The Transformer, the first sequence transduction model based entirely on attention, replacing the recurrent layers most commonly used in encoder-decoder architectures with multi-headed self-attention.

Model Architecture

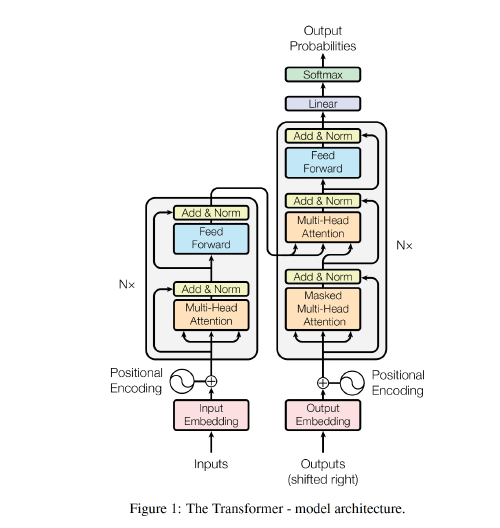
Encoder and Decoder Stacks
- Encoder: takes a sequence of symbols $(x_1,…,x_n)$ as input and returns a sequence of continuous representations $z = (z_1,…,z_n)$.
  - It consists of 6 identical layers, each with two sub-layers:
    1. a multi-head self-attention mechanism,
    2. a simple, fully connected feed-forward network with position-wise connection.
  - A residual connection is added around each of the two sub-layers, followed by layer normalization → the output of each sub-layer is $LayerNorm(x + Sublayer(x))$.
  - The output dimension of all sub-layers and embedding layers is $d_{model} = 512$.
- Decoder: generates an output sequence $(y_1,…, y_m)$ of symbols one element at a time based on $z$.
  - It consists of 6 identical layers.
  - A third sub-layer applies multi-head attention over the output of the encoder stack.
  - Residual connections are employed around each of the sub-layers, followed by layer normalization.
  - Masking is used to modify the self-attention sub-layer in the decoder stack, which prevents positions from attending to subsequent positions.
Attention
An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors.
- Scaled Dot-Product Attention
  - Input: queries and keys of dimension $d_k$, and values of dimension $d_v$
  - Compute the dot product of the query with all keys, then divide each by $\sqrt{d_k}$.
    - We scale the dot products by $1/\sqrt{d_k}$ to prevent large values of $d_k$ from pushing the softmax function into regions where it has extremely small gradients.
  - Apply a softmax function to obtain weights on the values.
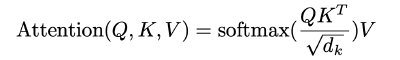
  Compared to additive attention, dot-product attention is faster and more space-efficient.
- Multi-Head Attention
  - Linearly project the queries, keys and values $h$ times with different linear projections to dimensions $d_k$, $d_k$ and $d_v$ respectively.
  - Perform the attention function in parallel, yielding $d_v$-dimensional output values. These are concatenated and projected once again.
  - Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions.
    - In this work we employ $h = 8$ parallel attention layers, or heads. For each of these we use $d_k = d_v = d_{model}/h = 64$.
  The Transformer uses multi-head attention in three different ways:
  1. The queries come from the previous decoder layer, and the memory keys and values come from the output of the encoder. This allows every position in the decoder to attend over all positions in the input sequence.
  2. The encoder contains self-attention layers, where all of the keys, values and queries come from the output of the previous layer in the encoder. So each position can attend to all positions in the previous layer of the encoder.
  3. Similarly, self-attention layers in the decoder allow each position to attend to all positions in the decoder up to and including that position. Illegal connections are masked out in the input of the softmax by setting them to −∞, and this is implemented inside of scaled dot-product attention.
Position-wise Feed-Forward Networks
Each layer in our encoder and decoder has a fully connected feed-forward network. This network is applied to each position separately and identically. It includes two linear transformations with a ReLU activation in between.
- The dimensionality of input and output is $d_{model} = 512$, and the inner-layer has dimensionality $d_{ff} =2048$.
Embeddings and Softmax
- Use learned embeddings to convert the input tokens and B to vectors of dimension $d_{model}$.
- Use the usual learned linear transformation and softmax function to convert the decoder output to predicted next-token probabilities.
Positional Encoding
- In order for the model to make use of the order of the sequence, we must inject some information about the relative or absolute position of the tokens in the sequence.
- Add “positional encodings” to the input embeddings at the bottoms of the encoder and decoder stacks. The positional encodings have the same dimension $d_{model}$ as the embeddings, so that the two can be summed.
  where $pos$ is the position and $i$ is the dimension.