BERT is designed to pre-train deep bidirectional representations from unlabeled text by jointly conditioning on both left and right context in all layers. As a result, the pre-trained BERT model can be fine-tuned with just one additional output layer to create state-of-the-art models for a wide range of tasks.
Awesome explanation: Li Hung-yi, Li Mu

2 existing strategies for applying pre-trained language representations to downstream tasks:
- Feature-based: includes the pre-trained representations as additional features.
- BERT vs. ELMo(feature-based): BERT uses Transformer; ELMo uses RNN
- Fine-tuning: is trained on the downstream tasks by simply fine-tuning all pre-trained parameters.
- BERT vs. GPT(fine-tuning): BERT is bidirectionall; GPT is unidirectional
- Unidirectional language models limit the choice of architectures used during pre-training; harmful for Q&A
BERT Overview
BERT uses:
- “masked language model” (MLM) pre-training objective: randomly masks some of the tokens from the input, and the objective is to predict the original vocabulary id of the masked word based only on its context.
- MLM objective enables the representation to fuse the left and the right context, which allows us to pre-train a deep bidirectional Transformer.
- “next sentence prediction” task: jointly pre-trains text-pair representations.
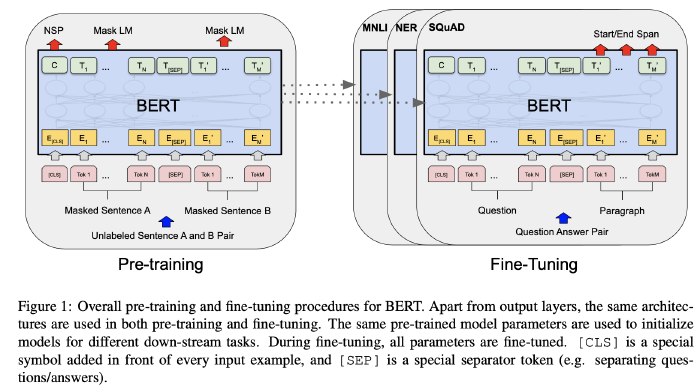
BERT has 2 steps in the framework:
- Pre-training: trained on unlabeled data over different pre-training tasks.
- Fine-tuning: first initialized with the pre-trained parameters, and all of the parameters are fine-tuned using labeled data from the downstream tasks.
- There is minimal difference between the pre-trained architecture and the final downstream architecture.
Model Architecture: BERT’s model architecture is a multi-layer bidirectional Transformer encoder based on Attention is All You Need.
- $BERT_{BASE}$ (L=12, H=768, A=12, Total Parameters=110M) & $BERT_{LARGE}$ (L=24, H=1024,A=16, Total Parameters=340M).
- L: the number of layers (i.e., Transformer blocks)
- H: the hidden size
- A: the number of self-attention heads
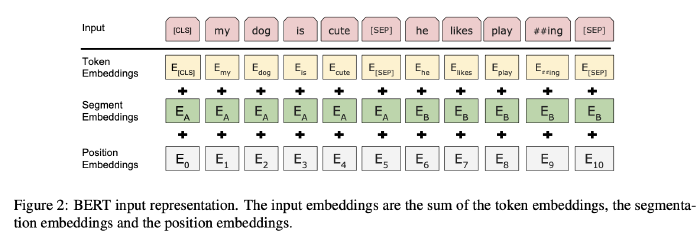
Input/Output Representations: the input representation can represent both a single sentence and a pair of sentences (e.g., ⟨ Question, Answer ⟩) in one token sequence.
- Differentiate the sentences in two ways: 1) separate them with a special token ([SEP]). 2) add a learned embedding to every token indicating whether it belongs to sentence A or sentence B.
- $E$: input embedding
- $C ∈ R^H$: the final hidden vector of the special [CLS] token
- $T_i ∈R^H$: the final hidden vector for the $i$-th input token.
- For a given token, its input representation is constructed by summing the corresponding token, segment, and position embeddings.
Pre-training BERT
pre-train BERT using two unsupervised tasks: Masked LM & Next Sentence Prediction (NSP)
Task #1: Masked LM
Mask 15% of all WordPiece tokens in each sequence at random, and then $T_i$ will be used to predict the original token with cross entropy loss.
The final hidden vectors corresponding to the mask tokens are fed into an output softmax (Linear Multi-class classifier) over the vocabulary.
If the i-th token is chosen, we replace the i-th token with:
- The
[MASK]token 80% of the time - A random token 10% of the time
- The unchanged i-th token 10% of the time.
- The

Task #2: Next Sentence Prediction (NSP)
Goal: to understands sentence relationships, we pre-train for a binarized next sentence prediction task.
- When choosing the sentences A and B for each pre- training example, 50% of the time B is the actual next sentence that follows A (labeled as IsNext), and 50% of the time it is a random sentence from the corpus (labeled as NotNext).
Fine-tuning BERT(How to use BERT?)
For each task, plug in the task- specific inputs and outputs into BERT and fine-tune all the parameters end-to-end.
At the output,
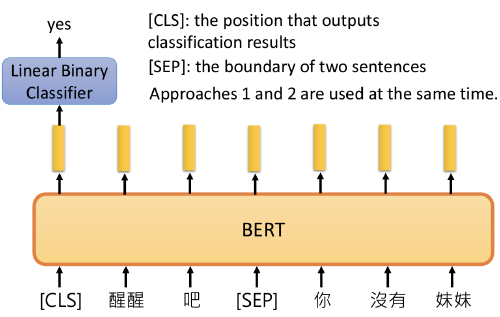
- For token-level tasks(sequence tagging or Q&A), the token representations are fed into an output layer.
- For classification (entailment or sentiment analysis), the [CLS] representation is fed into an output layer.
- The only new parameters introduced during fine-tuning are classification layer weights $W ∈ R^{K ×H}$ , where $K$ is the number of labels. Compute a standard classification loss with $C$ and $W$ , i.e., $\log(softmax(C W^T ))$.
